最近邻算法（kNN）详解

本文介绍kNN算法，其通过计算不同特征值距离分类样本。以电影分类为例说明原理，还讲解用Numpy实现该算法的步骤，包括数据预处理、模型训练等，也提及超参数搜索函数，最后展示了用sklearn封装好的方法实现，以及相关笔记内容。

原理介绍

简言之，kNN算法计算不同特征值之间的距离对样本进行分类。

OK，说完结论，懂的可以直接看代码部分了，如果不能理解的请听我娓娓道来~现在有这么一组数据

上面6个样本（电影）分别给出其特征（打斗镜头、拥抱镜头）和标签（电影类型）信息，现在给定一个新的样本，我们想知道这部电影的类型。由于是2维数据，我们可以用平面直角坐标系表示。

       

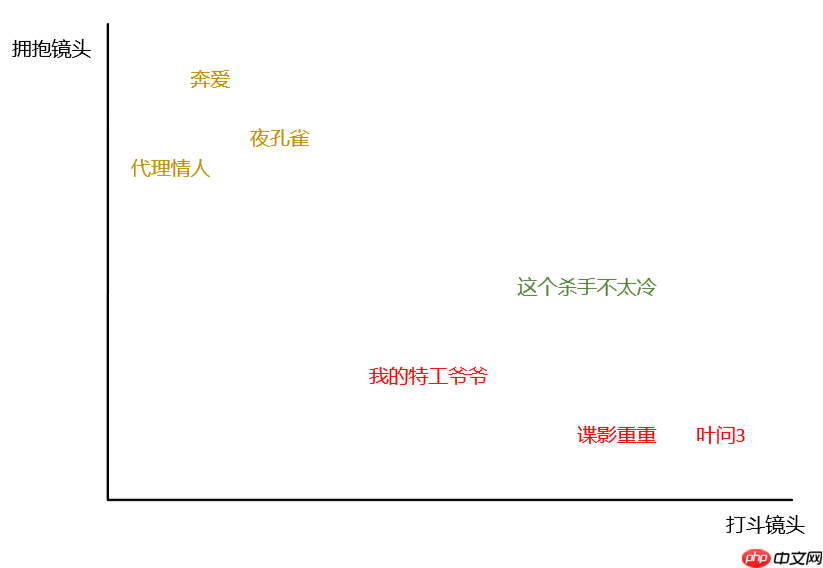
绿色的点是未知的，红色的黄色的点是已知的。kNN要做的就是计算未知的点到所有已知点的距离，根据距离进行排序。

$$D_{\text{谍影重重}}=\sqrt{(49-57{)}^2+(6-2{)}^2}\approx 8.94$$D谍影重重=(49−57)2+(6−2)2≈8.94

$$D_{\text{叶问}3}=\sqrt{(49-65{)}^2+(6-2{)}^2}\approx 16.49$$D叶问3=(49−65)2+(6−2)2≈16.49

$$D_{\text{我的特工爷爷}}=\sqrt{(49-21{)}^2+(6-4{)}^2}\approx 28.07$$D我的特工爷爷=(49−21)2+(6−4)2≈28.07

$$D_{\text{奔爱}}=\sqrt{(49-4{)}^2+(6-46{)}^2}\approx 60.21$$D奔爱=(49−4)2+(6−46)2≈60.21

$$D_{\text{夜孔雀}}=\sqrt{(49-8{)}^2+(6-39{)}^2}\approx 52.63$$D夜孔雀=(49−8)2+(6−39)2≈52.63

$$D_{\text{代理情人}}=\sqrt{(49-2{)}^2+(6-38{)}^2}\approx 56.86$$D代理情人=(49−2)2+(6−38)2≈56.86

排序后的数据如下，

我们在kNN算法中经常会听到说当k=3时、当k=5时...这里的k指的就是样本数。在这个例子中，当k=3时，前三个样本出现最多的电影类型是动作片，因此《这个杀手不太冷》样本也应该归为动作片。同样的，当k=5时，前5个样本出现最多的电影类型也是动作片（$\frac{3}{5}>\frac{2}{5}$53>52），因此样本也属于动作片。

上面提到的是2维数据，但是我们现实中处理的样本可能有3个甚至更多特征，我们无法用视觉来抽象这些特征，但是计算方法还是一样的，只不过根号里做差的数变多了而已。

       

代码实现——Numpy

机器学习算法的一般流程可以归为三步。

数据预处理加载数据交叉验证归一化模型训练模型验证

机器学习的任务就是从海量数据中找到有价值的信息， 所以在使用算法之前，我们要对数据进行预处理。

In [17]

# 1. 加载莺尾花数据集from sklearn import datasetsiris = datasets.load_iris()X = iris.datay = iris.target

登录后复制    

如果我们查看y标签信息会发现，它的前50个值为0，51—100的值为1，后50个值为2，如果直接交叉验证，取到的测试集数据可能都是label值为2的样本，这并不是我们想要的。所以在这之前，我们需要先对样本打乱顺序。zip()能将可迭代的对象打包成元组，利用 * 操作符可以将元组解压为列表。

In [18]

# 2. 实现交叉验证import numpy as npdef train_test_split(X, y, ratio=0.3):    # 乱序    data = list(zip(X, y))    np.random.shuffle(data)    X, y = zip(*data)    # 切割    boundary_X = int((1-ratio) * len(X))    boundary_y = int((1-ratio) * len(y))    # 将boundary_X和boundary_y之前的作为训练集    x_train = np.array(X[: boundary_X])    x_test = np.array(X[boundary_X:])    y_train = np.array(y[: boundary_y])    y_test = np.array(y[boundary_y:])    return x_train, x_test, y_train, y_testx_train, x_test, y_train, y_test = train_test_split(X, y)

登录后复制    

归一化主要有两种形式：0-1均匀分布和标准正态分布。

In [19]

# 3. 归一化def normalization(data):    return (data - data.min()) / (data.max() - data.min()) def standardization(data):    return (data - data.mean()) / data.std()x_train = standardization(x_train)x_test = standardization(x_test)

登录后复制    

kNN的“模型训练”有点不同于一般的模型训练过程，它们可能需要求一些参数，而kNN是计算未知点到已知点的距离。从严格意义上来说，这并不算是训练。

In [20]

# 4. 距离计算from collections import Counterclass KNNClassifier:    def __init__(self, k):        self._k = k        self._X_train = None        self._y_train = None    def fit(self, X_train, y_train):        self._X_train = X_train        self._y_train = y_train    # 预测X_predict样本的分类结果，这里的X_predict用的是交叉验证中的测试集    def predict(self, X_predict):        return np.array([self._predict(x) for x in X_predict])    def _predict(self, x):        # 计算输入样本_X_train到所有已知数据的距离        distances = np.sqrt(np.sum((self._X_train - x)**2, axis=1))        # 记录distances中前k个小的数对应的类别的出现次数        votes = Counter(self._y_train[np.argpartition(distances, self._k)[: self._k]])        # most_common(n)可以打印n个出现最多次元素的值和次数        predict_y = votes.most_common(1)[0][0]        return predict_y    # 计算准确率    def score(self, X_test, label):        y_predict = self.predict(X_test)        n_sample = len(label)        right_sample = 0        for i, e in enumerate(label):            if y_predict[i] == e:                right_sample += 1        return right_sample / n_sampleknn = KNNClassifier(k=3)knn.fit(x_train, y_train)knn.score(x_test, y_test)

登录后复制        

0.9555555555555556

登录后复制                

超参数搜索函数

kNN的参数不止是k，距离模式distype也是它的参数。对于k和distype这两种参数的组合，可能会有很多不同的结果，不妨设计一个超参数搜索函数来优化k和distype。

In [21]

class KNNClassifierSuper(KNNClassifier):    def __init__(self, k, distype):        super().__init__(k)        self.distype = distype    def _predict(self, x):        assert self.distype in ["1", "2", "3"], "Error distance type!"        if self.distype == "1":            distances = np.sum(abs(self._X_train - x), axis=1)        elif self.distype == "2":            distances = np.sqrt(np.sum((self._X_train - x)**2, axis=1))        else:            distances = np.max(abs(self._X_train - x), axis=1)        votes = Counter(self._y_train[np.argpartition(distances, self._k)[: self._k]])        predict_y = votes.most_common(1)[0][0]        return predict_y# ManhattanDistance —— "1"# EuclideanDistance —— "2"# ChebyshevDistance —— "3"for k in range(3, 15, 2):    for distype in range(1, 4):        knn = KNNClassifierSuper(k, str(distype))        knn.fit(x_train, y_train)        print("k = {}	distype = {}	score = {}".format(            k, distype, knn.score(x_test, y_test)))

登录后复制        

k = 3distype = 1score = 0.9555555555555556k = 3distype = 2score = 0.9555555555555556k = 3distype = 3score = 0.9777777777777777k = 5distype = 1score = 0.9777777777777777k = 5distype = 2score = 0.9777777777777777k = 5distype = 3score = 0.9777777777777777k = 7distype = 1score = 0.9777777777777777k = 7distype = 2score = 0.9777777777777777k = 7distype = 3score = 1.0k = 9distype = 1score = 0.9555555555555556k = 9distype = 2score = 0.9777777777777777k = 9distype = 3score = 1.0k = 11distype = 1score = 0.9777777777777777k = 11distype = 2score = 0.9555555555555556k = 11distype = 3score = 0.9777777777777777k = 13distype = 1score = 0.9777777777777777k = 13distype = 2score = 1.0k = 13distype = 3score = 0.9333333333333333

登录后复制        

代码实现——sklearn

上面我们用Numpy实现了交叉验证、归一化、距离计算等方法，这些在sklearn中都已经为我们封装好了。

In [31]

from sklearn.model_selection import train_test_split, GridSearchCVfrom sklearn import preprocessingfrom sklearn.neighbors import KNeighborsClassifier# 加载莺尾花数据iris = datasets.load_iris()X, y = iris.data, iris.target# 交叉验证x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.4)# 归一化x_train = preprocessing.scale(x_train)x_test = preprocessing.scale(x_test)# 距离计算 + 超参数搜索函数# p = 1 manhattan_distance # p = 2 euclidean_distance# arbitrary p minkowski_distance for k in range(3, 14, 2):    for p in range(1, 5):        knn = KNeighborsClassifier(n_neighbors=k, p=p)        knn.fit(x_train, y_train)        print("k = {}	p = {}	score = {}".format(            k, p, knn.score(x_test, y_test)))

登录后复制        

k = 3p = 1score = 0.9666666666666667k = 3p = 2score = 0.9833333333333333k = 3p = 3score = 0.9666666666666667k = 3p = 4score = 0.9666666666666667k = 5p = 1score = 0.9666666666666667k = 5p = 2score = 0.9833333333333333k = 5p = 3score = 0.9833333333333333k = 5p = 4score = 0.9833333333333333k = 7p = 1score = 0.9833333333333333k = 7p = 2score = 0.9833333333333333k = 7p = 3score = 0.9833333333333333k = 7p = 4score = 0.9833333333333333k = 9p = 1score = 0.9666666666666667k = 9p = 2score = 0.95k = 9p = 3score = 0.9666666666666667k = 9p = 4score = 0.9666666666666667k = 11p = 1score = 0.9666666666666667k = 11p = 2score = 0.95k = 11p = 3score = 0.9333333333333333k = 11p = 4score = 0.9333333333333333k = 13p = 1score = 0.9666666666666667k = 13p = 2score = 0.95k = 13p = 3score = 0.9166666666666666k = 13p = 4score = 0.9166666666666666

登录后复制        

笔记

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

ndarray计算的时候尽量用np的属性（np.sum()而不是sum）

---

ValueError: kth(=3) out of bounds (1)

计算距离的时候np.sum()需要指定axis=1，不然会直接对多维数组进行sum得到一个数值，在np.argpartition会出错。

---

np.sum()如果不指定axis是无法广播的，会直接返回数值

---

axis一种较好的理解方式是把他看成消除器。对于shape为（2L, 3L, 4L）的数组arr，np.sum(arr, axis=0)会返回shape为（3L, 4L）的数组，np.sum(arr, axis=1) 会返回shape为（2L, 4L）的数组，np.sum(arr, axis=0)会返回shape为（2L, 3L）的数组。