基于PaddlePaddle2.0-构建长短期记忆网络
发布时间:2025-07-29 编辑:游乐网
本文介绍用PaddlePaddle2构建长短期记忆网络模型。先讲引入时间步的单隐藏层、多隐藏层模型,说明隐藏层输出与输入及前一时间步输出的关系;再阐述长短期记忆网络通过输入门、遗忘门、输出门处理长跨度时间依赖。最后用该模型对IMDB电影评论做情感预测,经10轮训练,测试集准确率约84% - 85%。

PaddlePaddle2构建长短期记忆网络模型
作者:陆平
现实世界中,有一类问题是需要考虑时间顺序,比如,文本分类、机器翻译、语音识别、证券价格走势分析、宏观经济指标预测等。这类问题在推断下一个时间点的预测值时候,不仅需要依赖当前时间点的输入,还要依赖过去时间点的情况。利用长短期记忆网络模型可以用来处理具有长跨度时间依赖的问题。为了更易于理解,采用以下循序渐进的方式:首先需要理解如何在单隐藏层模型中引入时间步,其次是要理解如何构建引入时间步的多隐藏层模型,最后理解长短期记忆网络模型。
1. 引入时间步的单隐藏层模型
在解析模型之前,我们首先回顾一下多层感知机模型。多层感知机模型至少拥有1个隐藏层。给定一个大小为n的批量样本,特征数量为d,输入表示为X∈Rn×d,批量化的输入特征与权重相乘,之后用函数σ进行激活,隐藏层输出H∈Rn×h为:
H=σ(Xwxh+bh)
其中,wxh∈Rd×h,bh∈R1×h.如果是分类问题,设最终的类别数为c,接下来,把经过隐藏层激活的输出值进行线性转化,得到输出层的值。
O=Hwo+bo
其中,O∈Rn×c,wo∈Rh×c,bo∈R1×c.
最后,进行SoftMax运算,把输出值转变成概率分布。
现在我们在模型中引入时间步概念。时间步t的隐藏层输出由时间步t-1的隐藏层输出与时间步t的输入共同决定。
设时间步t的输入为Xt∈Rn×d,时间步t-1的隐藏层输出为Ht−1∈Rn×h,时间步t的隐藏层输出为:
Ht=σ(Xtwxh+Ht−1whh+bh)
其中,wxh∈Rd×h,whh∈Rh×h,bh∈R1×h.
接下来与多层感知机类似,把经过时间步t的隐藏层输出值进行线性转化,最后接SoftMax运算得到输出类别的概率。
2. 引入时间步的多隐藏层模型
下面我们来看拥有2个隐藏层的考虑时间步的多隐藏层模型。仍以构建多层感知机来理解,构造一个具有2个隐藏层的多层感知机。给定一个大小为n的批量样本,特征数量为d,输入表示为X∈Rn×d,批量化的输入特征与权重相乘,之后用函数σ进行激活,第一个隐藏层h1输出H(1)∈Rn×h1为:
H(1)=σ(Xwx,h1+bh1)
其中,wx,h1∈Rd×h1,bh1∈R1×h1。 之后,接第二个隐藏层h2,该层的输出H(2)∈Rn×h2为:
H(2)=σ(H(1)wh1,h2+bh2)
其中,wh1,h2∈Rh1×h2,bh2∈R1×h2。 设最终的类别数为c,接下来,把经过隐藏层激活的输出值进行线性转化,得到输出层的值。
O=H(2)wh2,o+bo
其中,O∈Rn×c,wh2,o∈Rh2×c,bo∈R1×c.
通过SoftMax运算,把输出值转变成概率分布。
参考多层感知机的构建方法,我们构造一个具有2个隐藏层的模型。 设时间步t的输入为Xt∈Rn×d,时间步t-1的隐藏层h1输出为Ht−11∈Rn×h1,时间步t的隐藏层h1输出为:
Ht(1)=σ(Xtwx,h1+Ht−1(1)wh1,h1+bh1)
其中,wx,h1∈Rd×h1,wh1,h1∈Rh1×h1,bh∈R1×h1.
接下来进入第二个隐藏层,时间步t的隐藏层h2输出Ht(2)∈Rn×h2为:
Ht(2)=σ(Ht(1)wh1,h2+Ht−1(2)wh2,h2+bh2)
其中,wh1,h2∈Rh1×h2,wh2,h2∈Rh2×h2,bh2∈R1×h2.
接下来,把经过第二个隐藏层的输出值进行线性转化,得到输出层的值。
Ot=Ht(2)wh2,o+bo
其中,Ot∈Rn×c,wh2,0∈Rh2×c,b0∈R1×c。最后通过SoftMax运算,把输出值转变成概率分布。
3. 长短期记忆网络
为了让模型具有处理具有长跨度时间依赖能力,长短期记忆网络模型通过输入门、遗忘门与输出门来选择性记忆时序信息。
长短期记忆网络模型的整体结构如下:
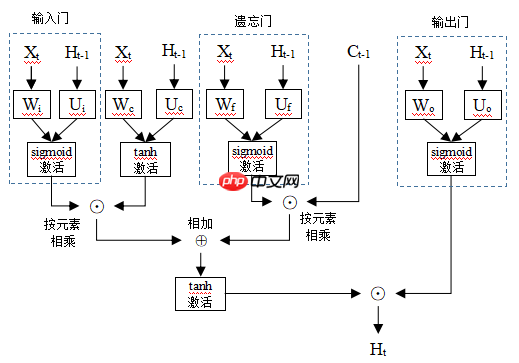
输入门(input gate)是用来衡量当前时间步输入的重要程度。给定一个大小为n的批量样本,输入特征数量为d,输出特征数量为q。时间步t的输入表示为Xt∈Rn×d,它与权重Wi∈Rd×q相乘,再加上时间步t-1的输出特征Ht−1∈Rn×q与权重Ui∈Rq×q乘积,接sigmoid函数激活,得到输出it∈Rn×q为:
it=σ(XtWi+Ht−1Ui)
遗忘门(foget gate)是用来衡量上一个时间步的单元状态值Ct−1∈Rn×q被记忆的程度。时间步t的输入Xt∈Rn×d与权重Wf∈Rd×q相乘,时间步t-1的输出特征Ht−1∈Rn×q与权重Uf∈Rq×q乘积,这两者相加后用sigmoid函数激活,得到输出ft∈Rn×q:
ft=σ(XtWf+Ht−1Uf)
输出门(output gate)是用来衡量单元状态值Ct∈Rn×q的暴露程度。时间步t的输入Xt∈Rn×d与权重Wo∈Rd×q相乘,时间步t-1的输出特征Ht−1∈Rn×q与权重Uo∈Rq×q乘积,这两者相加后用sigmoid函数激活,得到输出Ot∈Rn×q:
Ot=σ(XtWo+Ht−1Uo)
假设新的单元状态值是当前时间步输入信息与上一时间步输出的某种融合。时间步t的输入Xt∈Rn×d与权重Wc∈Rd×q相乘,时间步t-1的输出特征Ht−1∈Rn×q与权重Uc∈Rq×q乘积,这两者相加后用tanh函数激活。用以下式子表示:
C~t=tanh(XtWc+Ht−1Uc)
通过上面三个门,实现对时序信息进行选择性记忆与遗忘。时间步t的单元状态值Ct是以下两者的结合:一是上一时间步单元状态值Ct−1与记忆度ft按元素相乘,用来衡量被留下来的记忆。二是新的单元状态值C~t与重要度it按元素相乘,用来衡量新信息的重要性。
Ct=ft⨀Ct−1+it⨀C~t
最后,用输出门控制单元状态值Ct的暴露程度,得到输出Ht∈Rn×q,表示如下:
Ht=Ot⨀tanhCt
4. 基于LSTM模型的电影评论情感倾向预测
基于PaddlePaddle2.0基础API构建LSTM模型,利用互联网电影资料库Imdb数据来进行电影评论情感倾向预测。
In [1]
import numpy as npimport paddle#准备数据#加载IMDB数据imdb_train = paddle.text.datasets.Imdb(mode='train') #训练数据集imdb_test = paddle.text.datasets.Imdb(mode='test') #测试数据集#获取字典word_dict = imdb_train.word_idx#在字典中增加一个字符串word_dict[' '] = len(word_dict)#参数设定vocab_size = len(word_dict)embedding_size = 256hidden_size = 256n_layers = 2dropout = 0.5seq_len = 200batch_size = 64epochs = 10pad_id = word_dict[' ']#每个样本的单词数量不一样,用Padding使得每个样本输入大小为seq_lendef padding(dataset): padded_sents = [] labels = [] for batch_id, data in enumerate(dataset): sent, label = data[0].astype('int64'), data[1].astype('int64') padded_sent = np.concatenate([sent[:seq_len], [pad_id] * (seq_len - len(sent))]).astype('int64') padded_sents.append(padded_sent) labels.append(label) return np.array(padded_sents), np.array(labels)train_x, train_y = padding(imdb_train)test_x, test_y = padding(imdb_test) class IMDBDataset(paddle.io.Dataset): def __init__(self, sents, labels): self.sents = sents self.labels = labels def __getitem__(self, index): data = self.sents[index] label = self.labels[index] return data, label def __len__(self): return len(self.sents)train_dataset = IMDBDataset(train_x, train_y)test_dataset = IMDBDataset(test_x, test_y)train_loader = paddle.io.DataLoader(train_dataset, return_list=True, shuffle=True, batch_size=batch_size, drop_last=True)test_loader = paddle.io.DataLoader(test_dataset, return_list=True, shuffle=True, batch_size=batch_size, drop_last=True)#构建模型class LSTM(paddle.nn.Layer): def __init__(self): super(LSTM, self).__init__() self.embedding = paddle.nn.Embedding(vocab_size, embedding_size) self.lstm_layer = paddle.nn.LSTM(embedding_size, hidden_size, num_layers=n_layers, direction='bidirectional', dropout=dropout) self.linear = paddle.nn.Linear(in_features=hidden_size * 2, out_features=2) self.dropout = paddle.nn.Dropout(dropout) def forward(self, text): #输入text形状大小为[batch_size, seq_len] embedded = self.dropout(self.embedding(text)) #embedded形状大小为[batch_size, seq_len, embedding_size] output, (hidden, cell) = self.lstm_layer(embedded) #output形状大小为[batch_size,seq_len,num_directions * hidden_size] #hidden形状大小为[num_layers * num_directions, batch_size, hidden_size] #把前向的hidden与后向的hidden合并在一起 hidden = paddle.concat((hidden[-2,:,:], hidden[-1,:,:]), axis = 1) hidden = self.dropout(hidden) #hidden形状大小为[batch_size, hidden_size * num_directions] return self.linear(hidden)#以下使用PaddlePaddle2.0高层API进行训练与评估#封装模型model = paddle.Model(LSTM()) #用Model封装lstm模型#配置模型优化器、损失函数、评估函数model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()), paddle.nn.CrossEntropyLoss(), paddle.metric.Accuracy())#模型训练与评估model.fit(train_loader, test_loader, epochs=epochs, batch_size=batch_size, verbose=1)
Cache file /home/aistudio/.cache/paddle/dataset/imdb/imdb%2FaclImdb_v1.tar.gz not found, downloading https://dataset.bj.bcebos.com/imdb%2FaclImdb_v1.tar.gz Begin to downloadDownload finished/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/distributed/parallel.py:119: UserWarning: Currently not a parallel execution environment, `paddle.distributed.init_parallel_env` will not do anything. "Currently not a parallel execution environment, `paddle.distributed.init_parallel_env` will not do anything."/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/layers/utils.py:77: DeprecationWarning: Using or importing the ABCs from 'collections' instead of from 'collections.abc' is deprecated, and in 3.8 it will stop working return (isinstance(seq, collections.Sequence) and
The loss value printed in the log is the current step, and the metric is the average value of previous step.Epoch 1/10step 390/390 [==============================] - loss: 0.5087 - acc: 0.6604 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.5934 - acc: 0.7306 - 20ms/step Eval samples: 24960Epoch 2/10step 390/390 [==============================] - loss: 0.5487 - acc: 0.7938 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.4090 - acc: 0.7619 - 20ms/step Eval samples: 24960Epoch 3/10step 390/390 [==============================] - loss: 0.3800 - acc: 0.8056 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.4242 - acc: 0.8118 - 20ms/step Eval samples: 24960Epoch 4/10step 390/390 [==============================] - loss: 0.3291 - acc: 0.8685 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.3761 - acc: 0.8407 - 20ms/step Eval samples: 24960Epoch 5/10step 390/390 [==============================] - loss: 0.3086 - acc: 0.8935 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.2944 - acc: 0.8450 - 20ms/step Eval samples: 24960Epoch 6/10step 390/390 [==============================] - loss: 0.3261 - acc: 0.9089 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.2982 - acc: 0.8532 - 20ms/step Eval samples: 24960Epoch 7/10step 390/390 [==============================] - loss: 0.1245 - acc: 0.9227 - 58ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.5826 - acc: 0.8406 - 20ms/step Eval samples: 24960Epoch 8/10step 390/390 [==============================] - loss: 0.2069 - acc: 0.9365 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.4760 - acc: 0.8495 - 20ms/step Eval samples: 24960Epoch 9/10step 390/390 [==============================] - loss: 0.1122 - acc: 0.9460 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.3009 - acc: 0.8424 - 20ms/step Eval samples: 24960Epoch 10/10step 390/390 [==============================] - loss: 0.1645 - acc: 0.9540 - 59ms/step Eval begin...The loss value printed in the log is the current batch, and the metric is the average value of previous step.step 390/390 [==============================] - loss: 0.6611 - acc: 0.8377 - 20ms/step Eval samples: 24960
代码解释
经过10轮epoch训练,模型在测试数据集上的准确率大约为84%至85%。
相关阅读
MORE
+- 《猫里奥》通关图文攻略 03-29 《炎龙骑士团2》详细全攻略 03-10
- 《帝国时代4国家崛起》秘籍大全 08-23 《三国志9》详细全攻略心得 11-18
- 是男人就来征服海洋吧!史上十大经典航海游戏大盘点 03-17 《东吴霸王传2013》详细全关攻略 03-10
- 《臭作》之100%全完整攻略 08-04 《口袋妖怪红宝石》金手指代码大全 03-10
- DNF86版审判流圣骑士如何加点 07-04 《兰斯8》剧情攻略详细篇 03-10
- 《皇帝:龙之崛起》平民区及贵族区布局图一览 03-10 DNF女大枪86版刷图加点 03-21
- 《谜画之塔2》详细图文攻略 10-10 盘点十大画面精致的单机游戏 画面党最喜爱的游戏 03-10
- 《虚拟村庄4》图文全攻略 08-02 《英雄坛说》详细全攻略 03-10
- 《造梦西游2:十殿阎罗篇》BOSS档案及掉落装备全介绍及攻略 05-16 《兴唐传•瓦岗山异闻录》详细全攻略 03-10



























 湘公网安备
43070202000716号
湘公网安备
43070202000716号