参数空间对称性：统一深度学习与几何的理论框架

最近，加州大学圣迭戈分校与美国东北大学的研究人员联合发表了一篇系统性综述，深度剖析了深度神经网络中一个长期被忽略的数学结构：参数空间的对称性（parameter space symmetry）。

过去十年里，深度学习模型的规模从百万级参数的卷积网络，迅速扩展到拥有千亿甚至万亿参数的大语言模型，性能实现了质的飞跃。尽管如此，我们对这些模型为何能表现出如此强大的能力，仍缺乏根本性的理论解释。一个重要却常被忽视的因素在于：神经网络中存在大量“不同但等价”的参数配置——它们实现完全相同的输入输出映射，却让模型的优化轨迹与泛化分析变得异常复杂。

这篇长达三十页的综合论述揭示了对称性如何塑造损失函数的几何景观，影响优化过程的动态行为，并为理解深度学习提供了一个统一的数学框架。

论文链接：https://arxiv.org/abs/2506.13018
作者主页：https://b-zhao.github.io/

什么是参数空间对称性？

在神经网络中，不同的参数组合可能产生完全相同的输出结果。最直观的例子是神经元置换对称性：交换隐藏层中两个神经元及其对应的输入/输出权重，网络实现的函数关系依然保持不变。

图1：置换对称性示意。交换隐藏层中两个神经元及其关联的权重参数，函数输出保持不变

这类保持函数映射不变的参数变换，被称为参数空间对称性（parameter space symmetry）。

从数学角度看，它是一组保持损失函数L(θ)值不变的变换g，满足L(g·θ) = L(θ)。这些变换构成一个数学上的群结构，并在参数空间中定义了等价轨道：处于同一轨道上的参数都对应着相同的模型表达能力。

这一视角为理解损失曲面的连通性、平坦区域的普遍存在以及优化过程的动态特性提供了统一的理论语言。

除了离散的置换对称外，几乎所有常见的神经网络架构还具有连续对称性：

ReLU网络与BatchNorm/LayerNorm等归一化层具有正缩放对称性；线性层和注意力机制具有一般线性群（GL）对称性；Softmax函数具有平移不变性；其他结构（如径向基函数网络、某些特殊激活函数）也呈现出旋转或尺度变换对称性。

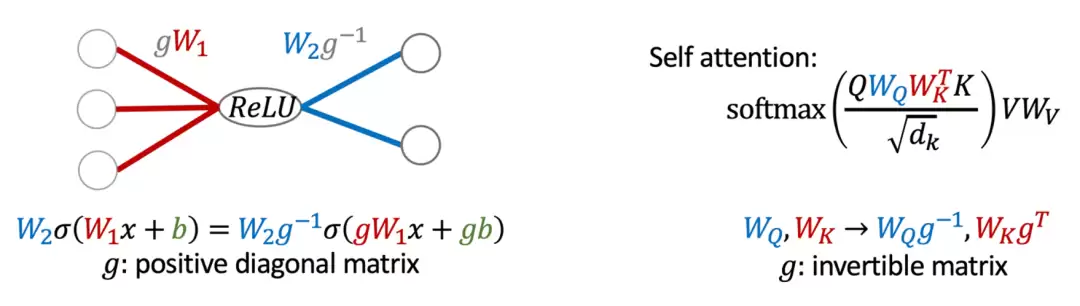
图2：（左）ReLU网络的缩放对称性：对输入权重与偏置按对角矩阵g进行缩放，同时对输出权重乘以g的逆矩阵，函数关系保持不变。（右）自注意力机制的一般线性对称性：键（WK）与查询（WQ）的线性变换g可以互相抵消，输出结果不变。

更重要的是，像Transformer这样的现代复杂架构，其对称性是其各个组件对称性的复合产物。例如，多头注意力机制同时具有每个头内部的广义线性对称性、头之间的排列对称性，以及与输出投影层相关的另一组线性对称性。

从平坦极值点到模式连通性：对称性如何塑造损失地形

对称性使得优化空间既拥有丰富的结构，又暗含严谨的数学规律。

连续对称性（如缩放变换）会将一个孤立的极值点“拉伸”成一个连续、平坦的极值流形。沿着这个流形移动，损失值始终保持恒定。这意味着网络损失的许多平坦方向并非来自更好的泛化能力，而是由结构对称性先天决定的。因此，传统上使用平坦度来衡量泛化能力的指标需要审慎解读。

此外，实践中观察到的“模式连通性”——即独立训练得到的模型往往能通过低损耗路径连接——其背后也有连续对称性的深刻影响。对称性天然地在参数空间中创造了连接功能等价参数的连续通道，从而解释了为何模型融合能够有效实现知识迁移。

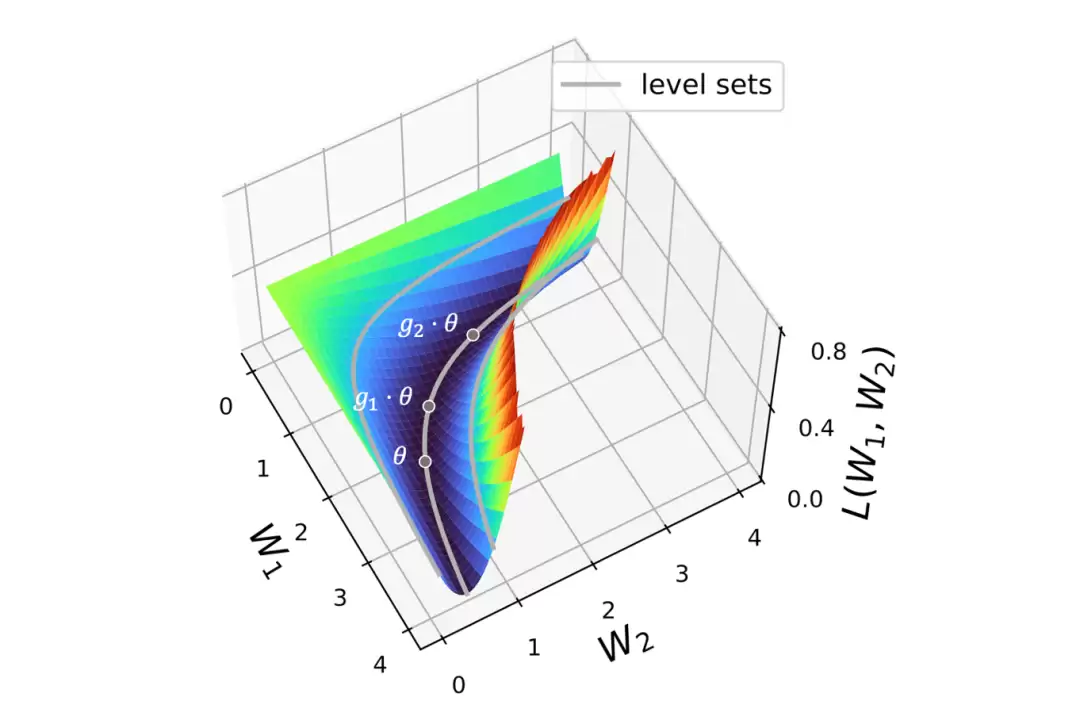
图3：连续对称性与平坦极值：不同的参数θ，g1·θ，g2·θ拥有相同的损失值，构成一条由对称变换生成的平坦优化轨迹。

离散对称性（如神经元置换）则会在参数空间的不同位置复制出大量功能完全相同的极值点“副本”。这让损失函数的几何景观更加复杂，其极值点的数量随着网络宽度呈阶乘级增长。

从几何到算法：利用对称性的优化方法

在对称群的作用下，即使两组参数产生完全相同的损失值，它们的梯度方向和大小也可能截然不同（图4左）。这意味着，即使两组参数在函数意义上等价，它们在训练过程中的优化轨迹也可能完全不同（图4右）。

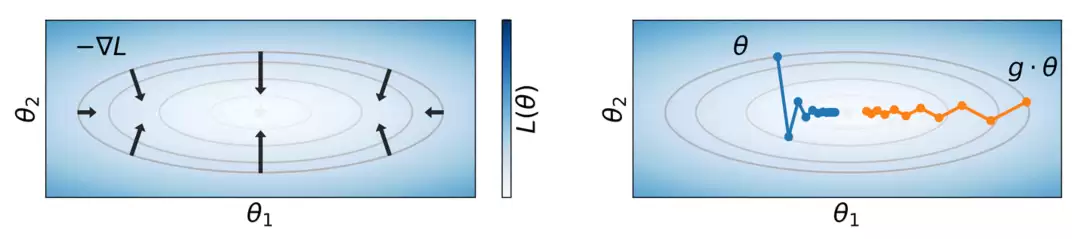
图4：相同损失值可能对应不同的梯度和训练轨迹。

这种“等损失、不同梯度”的现象为算法设计带来了新的思路。部分优化方法尝试在等价轨道中主动寻找梯度更优的点，以加速收敛或改善最终解的质量（图5左）；另一些方法则追求对参数初始点的对称变换不敏感，让优化结果对初始条件具有更好的鲁棒性（图5右）。

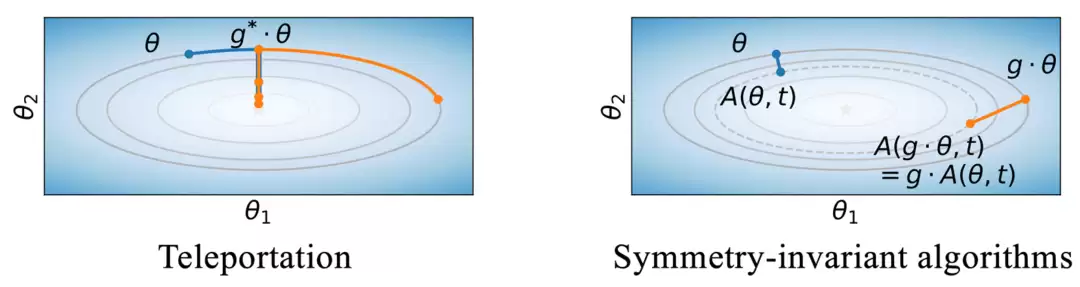
图5：两类应用对称性的优化算法策略

无论采用哪种思路，都表明对称性已成为理解和改进优化算法的重要理论工具。

从对称到守恒：学习动力学的新理解

连续对称性通常对应着某种守恒量——类似于物理学中的诺特定理揭示的深层联系。

在梯度流（gradient flow）的动态过程中，对称性使得某些量在整个训练期间保持恒定。例如，线性网络中相邻层的Gram矩阵差、ReLU网络中特定权重范数差等。

这些守恒量揭示了训练过程的稳定性，也帮助解释了优化算法的隐式偏好（implicit bias）：

不同的参数初始化对应着不同的守恒量初始值，进而影响最终的收敛点和泛化性能。也就是说，参数空间的对称结构从根本上决定了学习轨迹的演化路径与结果的统计分布。

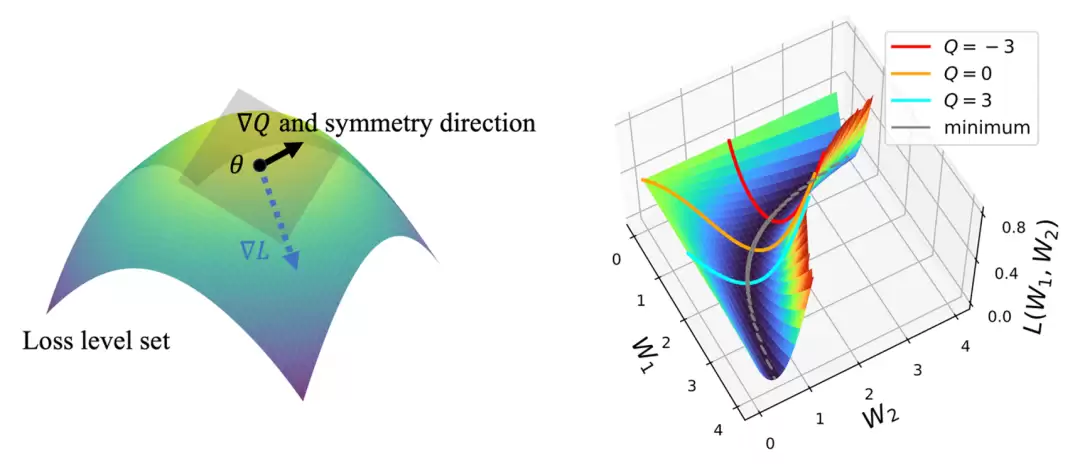
图6：对称性与守恒量的关系。（左）对称性方向上的梯度∇Q与损失梯度∇L正交，优化始终在损失水平集的切平面上进行。（右）守恒量在训练中保持不变，从而为梯度流轨迹与最终极值点提供了参数化坐标。

跨空间的关联：参数、特征与数据中的对称

参数空间中的对称性并非孤立存在，而是与数据空间和内部表征空间的对称性紧密相连。

当数据分布本身具有某种对称性（如旋转、平移或翻转不变性）时，训练得到的模型参数往往会继承并反映这些结构特征。

此外，在“权重空间学习”（Weight Space Learning）等新兴方向中，神经网络参数本身被作为输入数据。此时，对称性成为新的“数据结构”，支撑了等变元网络（equivariant meta-network）在模型性质分析、元学习和生成任务中的广泛应用。

图7：对称不变性与等变元网络：等变元网络可直接在模型权重上进行学习，被用于提升预测模型的泛化能力、优化学习过程，以及生成满足特定特征的新模型等任务。

展望：一个正在形成的研究领域

参数空间中的对称性广泛存在，为深度学习提供了一种新的数学语言，将模型的复杂行为与群论和几何中的成熟工具联系起来。

这一视角正在影响多个领域的实践：从加速优化与改善泛化，到模型融合、量子化与采样，再到新兴的权重空间学习与生成模型设计。对称性正在从理论概念转化为可操作的算法原则。

当然，对称性并非理解神经网络的唯一途径。但正如物理学、神经科学等学科为机器学习带来了新范式一样，数学化的视角让我们得以在这个完全人工的系统中寻找结构与规律，并由此开拓新的学习理论与算法思路。

免责声明

游乐网为非赢利性网站，所展示的游戏/软件/文章内容均来自于互联网或第三方用户上传分享，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系youleyoucom@outlook.com。

同类文章